Reductions are used to get a solution for some problem X, given you have a solution for another problem Y. A problem can be reduced to a problem at least as hard as itself. Otherwise, if the reductions worked the other way, i.e. reducing a problem to an easier problem, one could use these reductions to simplify all problems. Therefore, reducing Y to X implies X is at least as hard as Y. To prove X and Y are of the same complexity and none is harder than the other, there must exist a polynomial-time reduction from X to Y.
2-CNF falls in class P and therefore is decidable in polynomial time.
For all k-CNF (k>=3), the problem is NP-Complete. Since all these problems lie in the same complexity class, all of them must be reducible to each other.
Before we start with the proof, here are some useful information:
1. A CNF is satisfiable only if there exists a non-conflicting assignment to all its boolean variables that render the expression to true.
2. A CNF is a conjunction of disjunctions, represented as clauses separated by ∧.
(l1 V l2 V .. ln) ∧ .... (l1 V l2 V .. ln)
4. Each clause has literals separated by V.
5. Literal can be a boolean variable or a negation of it.
6. In a k-CNF, each clause has k literals.
In order to satisfy a CNF, all its clauses must be true. We, therefore, are interested in assignments that make a clause true.
For the proof, we will use the rule of resolution:
If (P → Q) is true and (Q → R) is true, then (P → R) is true.
If (a + b) and (b' + c) is true, then (a + c) is true.
PROOF:
1. Reducing 3-CNF to k-CNF
Let a clause in 3-CNF C = (l1 V l2 V l3)
add an extra variable y in a way its addition does not affect the clause.
Example:
(l1 V l2 V l3) = (l1 V l2 V l3 V y) ∧ (l1 V l2 V l3 V y')
[By resolution, LHS = RHS]
Keep padding the extra variable until you achieve k literals in each clause.
2. Reducing k-CNF to 3-CNF
Similarly, as above proof, keep breaking your clause with the rule of resolution until each clause has only 3 literals.
Let k be 4 and a clause in k-CNF, C = (l1 V l2 V l3 V l4)
C can be broken into two clauses C1 and C2
(l1 V l2 V l3 V l4) = (l1 V l2 V y) ∧ (y' V l3 V l4)
[By resolution, LHS = RHS]
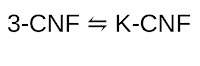 |
| 3-CNF <-> K-CNF |
2-CNF falls in class P and therefore is decidable in polynomial time.
For all k-CNF (k>=3), the problem is NP-Complete. Since all these problems lie in the same complexity class, all of them must be reducible to each other.
Before we start with the proof, here are some useful information:
1. A CNF is satisfiable only if there exists a non-conflicting assignment to all its boolean variables that render the expression to true.
2. A CNF is a conjunction of disjunctions, represented as clauses separated by ∧.
(l1 V l2 V .. ln) ∧ .... (l1 V l2 V .. ln)
4. Each clause has literals separated by V.
5. Literal can be a boolean variable or a negation of it.
6. In a k-CNF, each clause has k literals.
In order to satisfy a CNF, all its clauses must be true. We, therefore, are interested in assignments that make a clause true.
For the proof, we will use the rule of resolution:
If (P → Q) is true and (Q → R) is true, then (P → R) is true.
If (a + b) and (b' + c) is true, then (a + c) is true.
PROOF:
1. Reducing 3-CNF to k-CNF
Let a clause in 3-CNF C = (l1 V l2 V l3)
add an extra variable y in a way its addition does not affect the clause.
Example:
(l1 V l2 V l3) = (l1 V l2 V l3 V y) ∧ (l1 V l2 V l3 V y')
[By resolution, LHS = RHS]
Keep padding the extra variable until you achieve k literals in each clause.
2. Reducing k-CNF to 3-CNF
Similarly, as above proof, keep breaking your clause with the rule of resolution until each clause has only 3 literals.
Let k be 4 and a clause in k-CNF, C = (l1 V l2 V l3 V l4)
C can be broken into two clauses C1 and C2
(l1 V l2 V l3 V l4) = (l1 V l2 V y) ∧ (y' V l3 V l4)
[By resolution, LHS = RHS]